-

-
- INFORMATOR - ZAGADNIENIA
NIEOBOWIĄZUJĄCE NA MATURZE 2025 - DODATEK DO REPETYTORIUM
STEREOMETRIA - DARMOWY PORADNIK O NAUCE
- PLANSZE I ZADANIA INTERAKTYWNE
- PEWNIAKI MATURALNE
- TESTY ON-LINE
- MATURA Z MATEMATYKI 2026 ODPOWIEDZI
- ARKUSZE MATURALNE CKE
- TABLICE MATEMATYCZNE
- PODSTAWA PROGRAMOWA
- ZASADY MATURALNE - WAŻNE!
- KURS MATURALNY ON-LINE W FERIE

- WYPOŻYCZALNIA KSIĄŻEK ON-LINE
- ODBIERZ DARMOWĄ PŁYTĘ CD
- KURS EKSPRESOWY - INFORMACJE
- KURS EKSPRESOWY - ZAPISY
- KURS FERYJNY 2015
- WAŻNE INFORMACJE
- INFORMATOR - ZAGADNIENIA
-
SKLEPZAMÓWIENIA
GRUPOWE
UWAGA: 2018-04-10: W przypadku wystąpienia jakichkolwiek problemów z wykorzystaniem posiadanego kodu prosimy o przesłanie wiadomości na adres elitmat@elitmat.pl.
UWAGA: 2018-04-10: W przypadku wystąpienia jakichkolwiek problemów z wykorzystaniem posiadanego kodu prosimy o przesłanie wiadomości na adres elitmat@elitmat.pl.
Właściciel serwisu:
Firma Edukacyjno-Wydawnicza ELITMAT Dariusz Kulma
ul. Okrzei 7
05-300 Mińsk Mazowiecki
elitmat@elitmat.pl
Usługi płatności internetowych obsługuje Eurokoncept, grupa Dotpay.
Regulamin Usług.
Reklamacja usługi Premium.
MENU
LEKCJA 1 - Wyrażenia algebraiczne
LEKCJA 2 - Równania i nierówności liniowe
LEKCJA 3 - Równania i nierówności kwadratowe
LEKCJA 4 - Równania wielomianowe
LEKCJA 5 - Dowody z podzielnością
LEKCJA 6 - Wykazywanie nierówności
LEKCJA 7 - Równania wymierne i zadania tekstowe wykorzystujące równania wymierne
LEKCJA 8 - Własności funkcji
LEKCJA 9 - Zadania tekstowe
LEKCJA 10 - Ciąg arytmetyczny i geometryczny
LEKCJA 11 - Zależność między kątem środkowym i wpisanym
LEKCJA 12 - Kombinatoryka i prawdopodobieństwo
LEKCJA 13 - Logarytmy
LEKCJA 14 - Funkcje trygonometryczne
POZIOM PODSTAWOWY, LEKCJA 8
Własności funkcji
W dzisiejszej lekcji zajmiemy się odczytywaniem własności funkcji na podstawie wykresu.
Mówiąc o własnościach funkcji możemy określać:
- dziedzinę funkcji
- zbiór wartości funkcji
- monotoniczność funkcji, czyli czy funkcja jest rosnąca, malejąca czy stała i w jakich przedziałach
- miejsca zerowe
- znak funkcji, czyli w jakim przedziale funkcja jest ujemna, a w jakim dodatnia
- najmniejszą i największą wartość funkcji w przedziale
Korzystając z wykresu dowolnej funkcji możemy określić wszystkie z powyższych własności tej funkcji. Dotyczy to również funkcji liniowej i kwadratowej, ponieważ określając własności tych konkretnych funkcji, robimy to w taki sam sposób, jak w przypadku każdej innej funkcji.
WAŻNE:
Określając poszczególne własności koniecznie zwróć uwagę na końce przedziałów - czy jest otwarte czy zamalowane kółeczko na wykresie, ponieważ na tej podstawie decydujemy, czy piszemy otwarty czy zamknięty przedział.
Do omówienia wszystkich własności skorzystamy z poniższej planszy. Otwórz ją i na podstawie przykładu nr 1 przeanalizujemy wszystkie powyższe własności. Zwróć szczególną uwagę na informacje zapisane na niebieskim tle przy przykładzie na każdej z grafik poniżej, ponieważ dowiesz sie z nich, jak w praktyczny sposób określać dane własności.
DZIEDZINA FUNKCJI
Zaczniemy od dziedziny funkcji, czyli zbioru wszystkich argumentów.
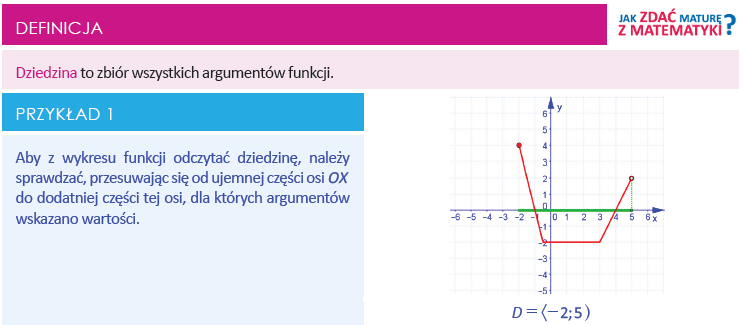
ZBIÓR WARTOŚCI
Następnie przechodzimy do zbioru wartości, czyli zbioru y-ów na osi OY.

MONOTONICZNOŚĆ FUNKCJI
Zapamiętaj, że jeśli mówimy o monotoniczności funkcji, to sprawdzamy, czy funkcja jest malejąca, rosnąca czy stała oraz czy w całej swojej dziedzinie, czy w przedziałach.
Jeśli funkcja jest rosnąca lub malejąca w co najmniej dwóch przedziałach, to pamiętaj, że nie możemy pomiędzy tymi przedziałami napisać znaku sumy, lecz każdy przedział określamy oddzielnie.
Określając monotoniczność funkcji, podajemy maksymalne przedziały monotoniczności, czyli przedziały domknięte, jeżeli dla argumentów, które są końcami przedziału, istnieje wartość funkcji.

MIEJSCE ZEROWE

ZNAK FUNKCJI, CZYLI DODATNIOŚĆ I UJEMNOŚĆ FUNKCJI
Jeżeli mamy określić znak funkcji, to oznacza, że mamy podać, w jakim przedziale zawartym w dziedzinie funkcja jest dodatnia, a w jakim ujemna.

WARTOŚĆ NAJWIĘKSZA I WARTOŚĆ NAJMNIEJSZA W PRZEDZIALE
Mówiąc o wartości najmniejszej i największej najczęściej będziemy ją określać w konkretnym przedziale. Pamiętaj, że może zdarzyć się tak, że takie wartości nie istnieją.

Przeanalizowaliśmy dokładnie pierwszy przykład z planszy. W podobny sposób określ własności pozostałych funkcji w kolejnych przykładach.
Możesz skorzystać z poniższego zadania lub przejść do kolejnych przykładów w planszy interaktywnej.
Zadanie 1. Na podstawie wykresu funkcji określ:
• dziedzinę funkcji,
• zbiór wartości funkcji,
• monotoniczność funkcji,
• miejsca zerowe,
• przedziały, w których funkcja jest dodatnia i przedziały, w których jest ujemna,
• najmniejszą i największą wartość funkcji.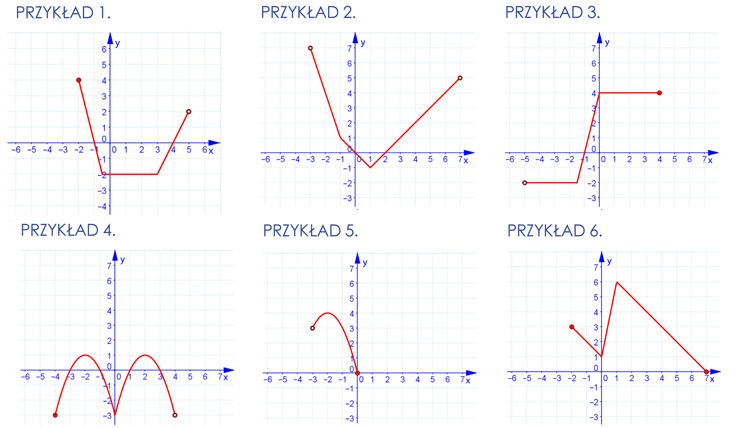
Następnie dla utrwalenia zrób jeszcze poniższe zadania.
Zadanie 2. Na podstawie wykresu funkcji określ:
• dziedzinę funkcji,
• zbiór wartości funkcji,
• maksymalne przedziały monotoniczności,
• miejsca zerowe,
• przedziały, w których funkcja jest dodatnia i przedziały, w których jest ujemna.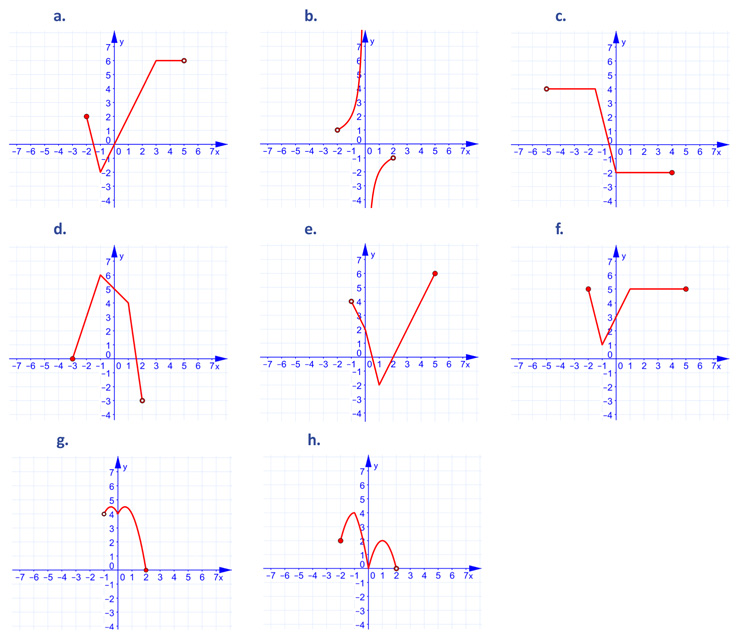
Zadanie 3. (3 pkt.) Na podstawie wykresu funkcji określ dziedzinę, zbiór wartości, miejsce zerowe oraz najmniejszą wartość funkcji.
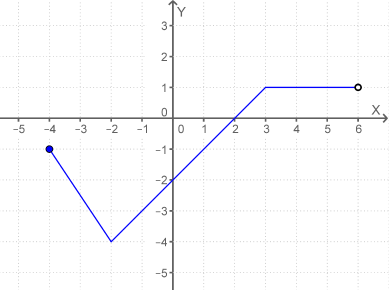
Zadanie 4. Na podstawie wykresu funkcji określ dziedzinę, zbiór wartości funkcji oraz maksymalne przedziały monotoniczności. 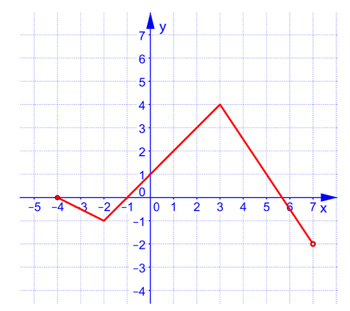
odpowiedź >>>
•\[ D \in \langle -4; 7 ) \]
•\[y \in (-2; 4 \rangle \]
• funkcja rosnąca\[f(x) \]dla\[x \in \langle -2;3 \rangle \]
• funkcja malejąca\[f(x) \]dla\[x \in \langle -4;-2 \rangle \]oraz\[x \in \langle 3; 7 ) \]Zadanie 5. (3 pkt.) Na podstawie wykresu funkcji określ dziedzinę, zbiór wartości oraz maksymalne przedziały monotoniczności. Zróbmy jeszcze kilka zadań maturalnych.
Zadanie 6. (2 pkt.) (Maj 2011) Na rysunku przedstawiono wykres funkcji \[f\].
Odczytaj z wykresu i zapisz:
a. zbiór wartości funkcji\[f\]
b. przedział maksymalnej długości, w którym funkcja\[f\]jest malejąca.Zadanie 7. (2 pkt.) (Maj 2013) Na rysunku przedstawiony jest wykres funkcji \[f(x)\]określonej dla\[x \in \langle -7;\;8 \rangle \].
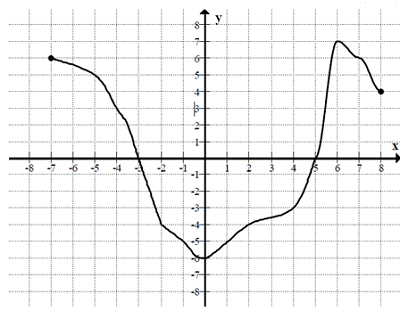
Odczytaj z wykresu i zapisz:a. największą wartość funkcji \[f\]b. zbiór rozwiązań nierówności \[f(x) < 0 \]W kolejnym zadaniu nie mamy narysowanego wykresu, więc należy najpierw narysować wykres funkcji liniowej y = 3x - 4, zaznaczyć przedział <-2;2>, a następnie odczytać zbiór wartości dla tego przedziału argumentów.
Zadanie 8. (1 pkt.) (Czerwiec 2014) Funkcja \[f\]jest określona wzorem\[f(x)=3x-4\]dla każdej liczby z przedziału\[\langle -2; \; 2 \rangle \]. Zbiorem wartości tej funkcji jest przedział:TEST
Na koniec rozwiąż jeszcze osiem zadań testowych. Sprawdź, co już potrafisz :)
PODSUMOWANIE nr 8
W dzisiejszym podsumowaniu sięgamy do zadań sprzed tygodnia, czyli z początku kursu, ale dzięki systematycznemu powtarzaniu nie powinieneś mieć z nimi problemu. Wśród zadań znajdziesz również zadania z matur CKE z poprzednich lat.

MATURA
2026
Z MATEMATYKI





 Kasia, 2016-07-05
Kasia, 2016-07-05 







 kliknij obok przycisk "dotpay" obok wybranej opcji i wykonaj szybką płatność.
kliknij obok przycisk "dotpay" obok wybranej opcji i wykonaj szybką płatność.
 wyślij krótki SMS na numer podany w tabeli obok wybranej opcji.
wyślij krótki SMS na numer podany w tabeli obok wybranej opcji.
 otwórz ->
otwórz ->
 otwórz ->
otwórz ->