ZAMKNIJ   X

IX Ogólnopolski Kongres Innowacyjnych Nauczycieli Matematyki Online

 

Książka ta jest wynikiem wieloletniej pracy z młodzieżą autora, Dariusza Kulmy, który dzięki doświadczeniom związanym z nauczaniem zarówno osób zdolnych, jak i bardzo słabych i nie lubiących matematyki, opracował własny system nauczania tego przedmiotu, dzięki któremu, jak twierdzą jego uczniowie, można polubić, a przede wszystkim zrozumieć matematykę. Prowadzi on zajęcia z maturzystami zarówno na poziomie podstawowym jak i rozszerzonym, a średni wynik zdobyty przez nich na maturze w 2012 roku (aż 89,69%) potwierdza skuteczność jego metod. Książka przeznaczona jest dla maturzystów przygotowujących się do maturyz matematyki na poziomie podstawowym.

książka, jak zdać maturę z matematyki, Najprostsza droga do osiągnięcia sukcesu w 10 dni nie tylko dla humanistów, obowiązkowa matura z matematyki

Witam, Pana działalność umożliwia tysiącom maturzystów dostanie się na wymarzone studia związane z matematyką, lub po prostu zdanie tego przedmiotu na egzaminie końcowym. Niestety, obecnie nauczycielom matematyki bardzo trudno jest trafić do swoich uczniów, szczególnie w technikum, gdzie nie wszyscy uczniowie pracują tak ciężko jak ludzie z ranking(...) więcej

Norbert T., 2015-11-14
Inne osoby kupiły także
-5%

Kalkulator Vector CH-265
-30%

KOSZULKA MĘSKA "Love math", rozmiar: XL (czerwona)
Aby uczestniczyć w WYZWANIU MATURALNYM zaloguj się na swoje konto w STREFIE MATURZYSTY.
Jeżeli logujesz się pierwszy raz to wymagana będzie prostej rejestracji konta.
Dostęp do lekcji z wyzwania wymaga podania na koncie kodu z Twojej książki.
Jeżeli posiadasz aktywny kod do STREFY PREMIUM, wpisz go w to pole aby aktywować dostęp:
STREFA NAUCZYCIELA
ZALOGUJ
  /   STREFA MATURZYSTY
ZALOGUJ

UWAGA: 2018-04-10: W przypadku wystąpienia jakichkolwiek problemów z wykorzystaniem posiadanego kodu prosimy o przesłanie wiadomości na adres elitmat@elitmat.pl.



UWAGA! Kod ważny tylko dla JEDNEJ OSOBY. Próba użycia kodu przez inną osobę spowoduje ZABLOKOWANIE DOSTĘPU.
Jeżeli masz już kod możesz wpisać go w to miejsce:   


 
Aby uzyskać przez szybką płatność DotPay dostęp do materiałów PREMIUM:
  kliknij obok przycisk "dotpay" obok wybranej opcji i wykonaj szybką płatność.
  kod dostępu zostanie wyświetlony po poprawnym zakończeniu transakcji i wysłany na podany adres e-mail.
Otrzymany kod wpisz w pole pod tabelką. 		  Aby uzyskać SMSem dostęp do materiałów PREMIUM:
  wyślij krótki SMS na numer podany w tabeli obok wybranej opcji.
  w zwrotnej widaomości sms otrzymasz kod dostępu do testów. Otrzymany kod wpisz w pole pod tabelką.
Usługa SMS dostępna w sieciach T-mobile, Plus, Play, Orange.
Kod na 3 miesiące
koszt: 37,97 zł
(rabat 20%) 47,46 zł
 
Kod na pół roku
koszt: 49,97 zł
(rabat 20%) 62,46 zł
 
Podane ceny usług są cenami brutto.

UWAGA: 2018-04-10: W przypadku wystąpienia jakichkolwiek problemów z wykorzystaniem posiadanego kodu prosimy o przesłanie wiadomości na adres elitmat@elitmat.pl.



UWAGA! Kod ważny tylko dla JEDNEJ OSOBY. Próba użycia kodu przez inną osobę spowoduje ZABLOKOWANIE DOSTĘPU.
Aby uzyskać dostęp do serwisu, musisz wprowadzić kod:   

Właściciel serwisu:
Firma Edukacyjno-Wydawnicza ELITMAT Dariusz Kulma
ul. Okrzei 7
05-300 Mińsk Mazowiecki
elitmat@elitmat.pl

Usługi płatności internetowych obsługuje Eurokoncept, grupa Dotpay.
Regulamin Usług.
Reklamacja usługi Premium.


MENU

LEKCJA 1 - Wartość bezwzględna
LEKCJA 2 - Przekształcanie wykresu funkcji - odczytywanie liczby rozwiązań
LEKCJA 3 - Wielomiany - zadania z parametrem
LEKCJA 4 - Granice ciągów
LEKCJA 5 - Dowody z podzielnością
LEKCJA 6 - Podsumowanie lekcji 1-5
LEKCJA 7 - Wykazywanie nierówności
LEKCJA 8 - Zadania optymalizacyjne z wykorzystaniem funkcji kwadratowej
LEKCJA 9 - Równania kwadratowe z parametrem z wykorzystaniem wzorów Viete'a
LEKCJA 10 - Kombinatoryka i prawdopodobieństwo
LEKCJA 11 - Pochodne i ich zastosowanie, m.in. przedziały monotoniczności, ekstrema lokalne, styczne do wykresu, optymalizacja
LEKCJA 12 - Podsumowanie lekcji 1-11
LEKCJA 13 - Własności ciągów - arytmetycznego i geometrycznego
LEKCJA 14 - Równania trygonometryczne


POZIOM ROZSZERZONY, LEKCJA 4



Granice ciągów



Dziś omówimy granice ciągów. Jedno z takich zadań prawie na pewno znajdzie się w arkuszu maturalnym z poziomu rozszerzonego. Na początek trochę teorii z przykładami. Zwróć uwagę na trzy podstawowe przypadki, jakie mogą wystąpić przy obliczaniu granic. 

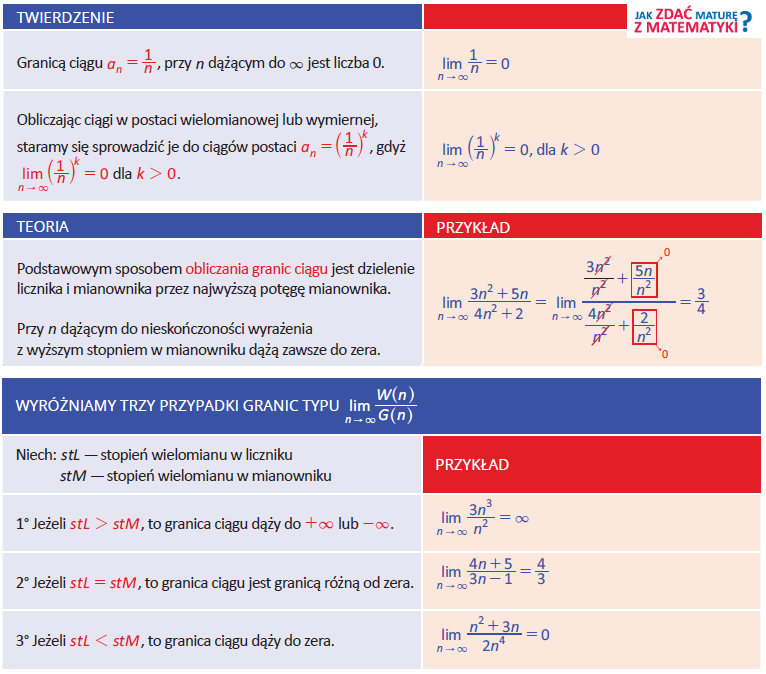
Przeanalizuj jeszcze jeden przykład.

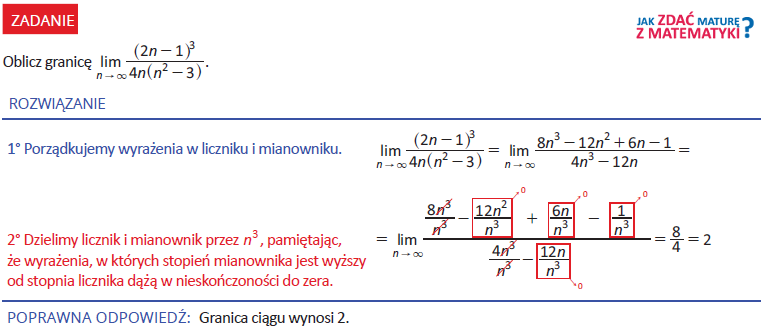
A teraz kilka przykładów. Rozwiązanie każdego z nich znajdziesz na planszy interaktywnej.

Zadanie 1. Oblicz granicę ciągów.
a.
\[ \lim_{n\to\infty} \frac{4n^2+5n}{2n^2+6n} \]
b.
\[ \lim_{n\to\infty} \frac{(n-1)(n^2+n+1)}{(n-4) \cdot (n-3)} \]
c.
\[ \lim_{n\to\infty} \frac{1-2n^2 +3n^3 - 4n^4}{n^4 - n^3 +n^2 -n+1} \]
d.
\[ \lim_{n\to\infty} \sqrt{\frac{8n+1}{2n+3}}\]
e.
\[ \lim_{n\to\infty} \frac{(4n-1)^3}{n(3n-1)(2n+3)} \]
f.
\[ \lim_{n\to\infty} \left(\frac{2n+1}{3n^2+4} \right)^4 \]
   

Teraz przejdziemy do zadań trochę trudniejszych. W pierwszym z nich wykorzystaj sumę ciągu arytmetycznego, a w drugim sumę szeregu geometrycznego. Rozwiązania sprawdź na planszach interaktywnych.

Zadanie 2. Oblicz granicę ciągu
\[ \lim_{n\to\infty} \frac{1+2+3+ \ldots+n}{n^2}\]
.
   
Zadanie 3. (2 pkt.) Oblicz granicę ciągu
\[ \lim_{n\to\infty} \frac{n+\frac{n}{2}+\frac{n}{4}+\frac{n}{8}+ \ldots}{\sqrt{4n^2+5n}}\]
.
otwórz ->
odpowiedź >>>    

Kolejne zadanie na dziś będzie zadaniem z parametrem. Przeanalizuj, korzystając z grafiki lub planszy.

Granica ciągu z parametrem 1

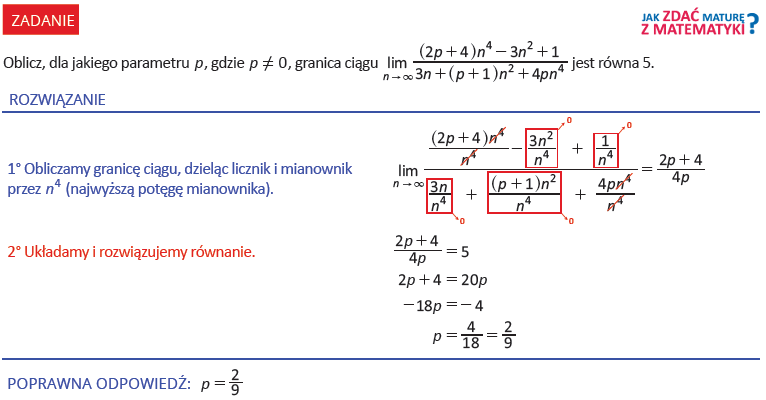
Następne zadanie wykonaj samodzielnie i sprawdź swoje rozwiązanie na planszy.

Zadanie 4. Oblicz, dla jakiego parametru
\[ p \not= 0 \]
granica ciągu
\[\lim_{n\to\infty} \frac{(5p-2)n^4+3n^3-4n}{n^2+3pn^3+(4p+11)n^4}\]
jest równa
\[\frac23 \]
.
   

PODSUMOWANIE nr 4

Dzisiejsze podsumowanie obejmuje 7 zadań, w tym zadanie z propozycji CKE oraz z matury z maja 2015. Powodzenia :)

Test sprawdzający - uruchom ->


Oferta wynajmu banera

MATURA

2025

Z MATEMATYKI