-

-
- INFORMATOR - ZAGADNIENIA
NIEOBOWIĄZUJĄCE NA MATURZE 2023 (liceum) - INFORMATOR - ZAGADNIENIA
NIEOBOWIĄZUJĄCE NA MATURZE 2023 (technikum) - DARMOWY PORADNIK O NAUCE
- PLANSZE I ZADANIA INTERAKTYWNE
- PEWNIAKI MATURALNE
- WYZWANIE MATURALNE >
- KSIĄŻKI ON-LINE
- TESTY ON-LINE
- MATURA Z MATEMATYKI 2024 ODPOWIEDZI
- ARKUSZE MATURALNE CKE
- TABLICE MATEMATYCZNE
- PODSTAWA PROGRAMOWA
- ZASADY MATURALNE - WAŻNE!
- KURS MATURALNY ON-LINE W FERIE

- WYPOŻYCZALNIA KSIĄŻEK ON-LINE
- ODBIERZ DARMOWĄ PŁYTĘ CD
- KURS EKSPRESOWY - INFORMACJE
- KURS EKSPRESOWY - ZAPISY
- KURS FERYJNY 2015
- WAŻNE INFORMACJE
- INFORMATOR - ZAGADNIENIA
-
SKLEPZAMÓWIENIA
GRUPOWE
LEKCJA PRZYKŁADOWA
DZIEŃ 2
Dziś zajmiemy się powtórzeniem POTĘG i PIERWIASTKÓW, NOTACJI WYKŁADNICZEJ i UŁAMKÓW OKRESOWYCH.
POTĘGI I PIERWIASTKI
Zaczynamy od przypomnienia definicji potęgi i pierwiastka - str. 24.

Przy pierwiastku stopnia nieparzystego (np. stopnia trzeciego) musisz pamiętać, że liczba pod pierwiastkiem może być również ujemna. Często to umyka, a to bardzo istotna informacja.
Powtarzając potęgi i pierwiastki, musimy przede wszystkim powtórzyć WZORY (TWIERDZENIA), dzięki którym będziemy mogli rozwiązywać trudniejsze zadania, w których trzeba będzie skorzystać z kilku wzorów po kolei.
Na początek przypomnij sobie wszystkie wzory i przeanalizuj ich zastosowanie na konkretncyh przykładach.
POTĘGI O TAKICH SAMYCH PODSTAWACH

Więcej przykładów znajdziesz w planszy, która dostępna jest w formie JPG oraz interaktywnej.
Przejdź do planszy:
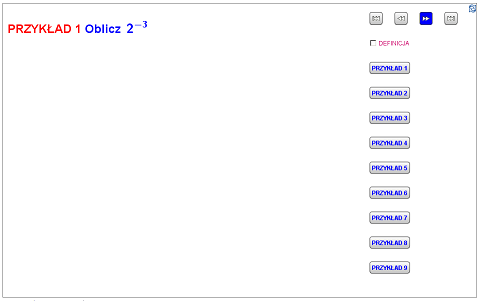
POTĘGI O WYKŁADNIKU CAŁKOWITYM UJEMNYM
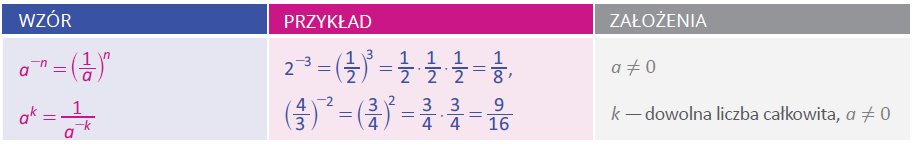
Więcej przykładów znajdziesz w planszy, która dostępna jest w formie JPG oraz interaktywnej.
Przejdź do planszy:
 http://jakzdacmaturezmatematyki.pl/plansze/potegi-o-wykladniku-calkowitym-ujemnym-przyklady
http://jakzdacmaturezmatematyki.pl/plansze/potegi-o-wykladniku-calkowitym-ujemnym-przyklady
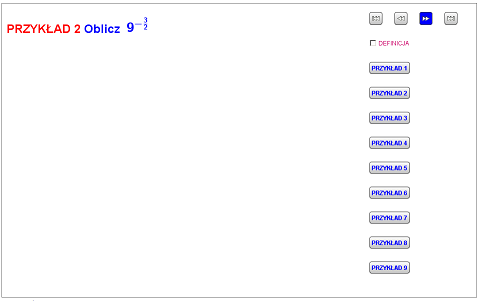
POTĘGI O WYKŁADNIKU WYMIERNYM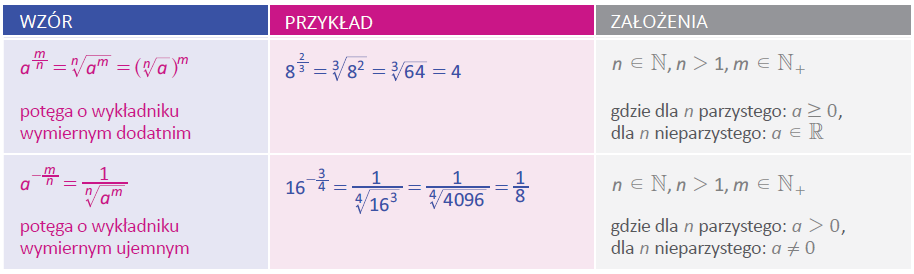
Więcej przykładów znajdziesz w planszy, która dostępna jest w formie JPG oraz interaktywnej.
Przejdź do planszy:
 http://jakzdacmaturezmatematyki.pl/plansze/potegi-o-wykladniku-wymiernym-przyklady
http://jakzdacmaturezmatematyki.pl/plansze/potegi-o-wykladniku-wymiernym-przyklady
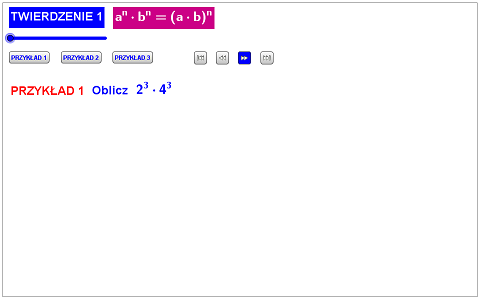
POTĘGI O TAKIM SAMYM WYKŁADNIKU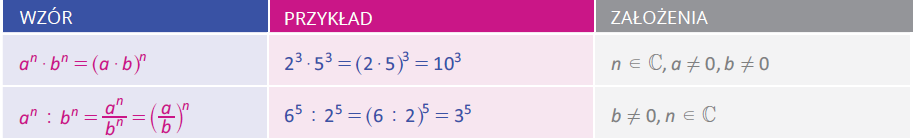
Więcej przykładów znajdziesz w planszy, która dostępna jest w formie JPG oraz interaktywnej.
Przejdź do planszy:
 jakzdacmaturezmatematyki.pl/plansze/wlasnosci-poteg-o-tym-samym-wykladniku-wzory-z-przykladami
jakzdacmaturezmatematyki.pl/plansze/wlasnosci-poteg-o-tym-samym-wykladniku-wzory-z-przykladamiPIERWIASTKI
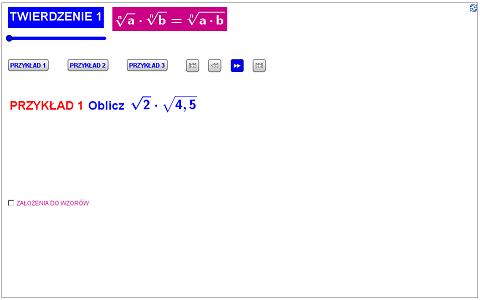
Teraz przypomnij sobie wzory dotyczące pierwiastków.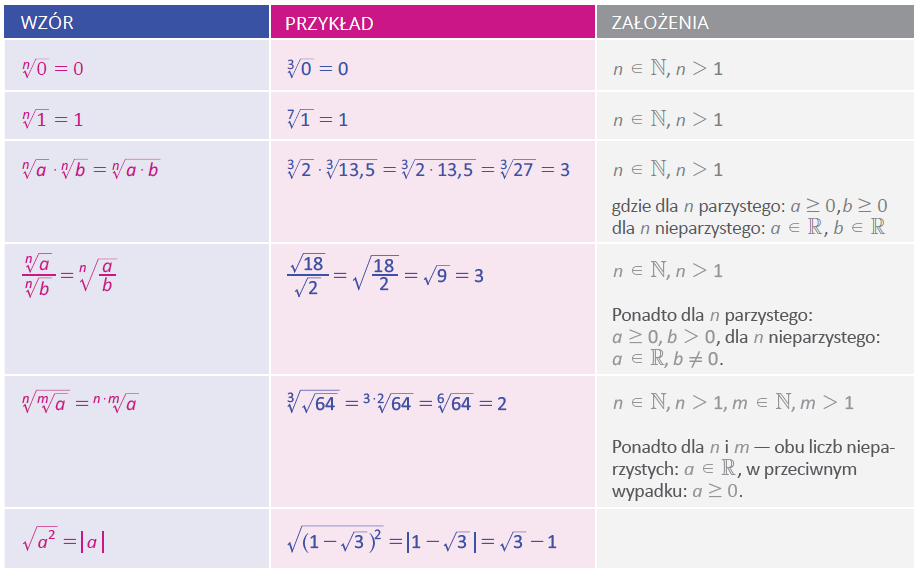
Więcej przykładów znajdziesz w planszy, która dostępna jest w formie JPG oraz interaktywnej.
Przejdź do planszy:
 http://jakzdacmaturezmatematyki.pl/plansze/pierwiastki-tego-samego-stopnia-wzory-z-przykladami
http://jakzdacmaturezmatematyki.pl/plansze/pierwiastki-tego-samego-stopnia-wzory-z-przykladamiPowtórzyłeś podstawowe wzory dotyczące potęg i pierwiastków. Teraz wykonaj zadania z książki od 16 do 24. Pamiętaj, żeby przeanalizować dokładnie pierwsze z każdej trójki zadań, a nastepnie samodzielnie wykonać kolejne dwa zadania.
Dla przećwiczenia rozwiąż jeszcze kilka poniższych zadań:
 http://jakzdacmaturezmatematyki.pl/zadania/potegi-matura-listopad-2009
http://jakzdacmaturezmatematyki.pl/zadania/potegi-matura-listopad-2009 http://jakzdacmaturezmatematyki.pl/zadania/potegi-matura-sierpien-2012
http://jakzdacmaturezmatematyki.pl/zadania/potegi-matura-sierpien-2012 http://jakzdacmaturezmatematyki.pl/zadania/potegi-pierwiastki-matura-p-czerwiec-2013
http://jakzdacmaturezmatematyki.pl/zadania/potegi-pierwiastki-matura-p-czerwiec-2013
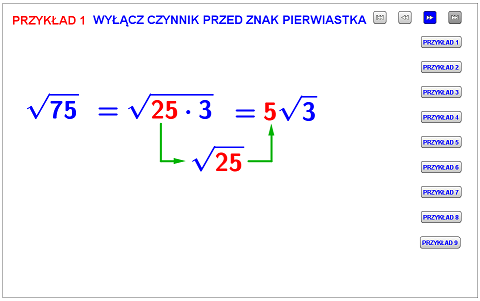
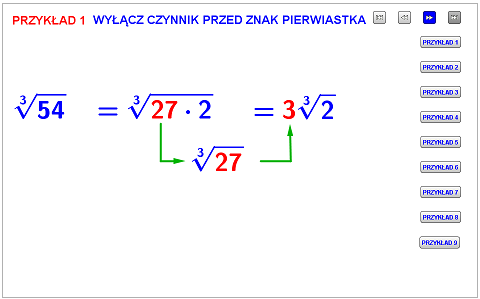
WYŁĄCZANIE CZYNNIKA PRZED ZNAK PIERWIASTKAWyłączanie czynnika przed znak pierwiastka to czynność, z którą na pewno dobrze sobie radzisz. Gdybyś jednak potrzebował przypomnienia, to w poniższych planszach możesz wykonać kilka przykładów z wyłączaniem czynnika przed znak pierwiastka stopnia drugiego i trzeciego.
Przejdź do planszy:
 http://jakzdacmaturezmatematyki.pl/plansze/wylaczanie-czynnika-przed-znak-pierwiastka-kwadratowego
http://jakzdacmaturezmatematyki.pl/plansze/wylaczanie-czynnika-przed-znak-pierwiastka-kwadratowegoPrzejdź do planszy:
Następnie zrób zadania od 25 do 27 z książki (str. 30)
NOTACJA WYKŁADNICZA
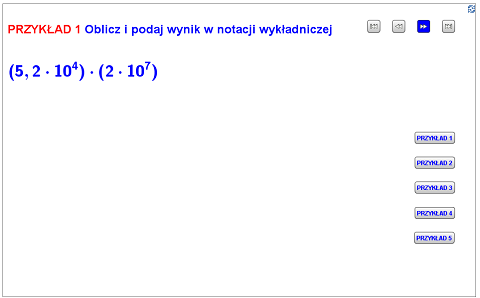
Na początek przypomnienie, jaki zapis nazywamy notacją wykładniczą. Najprościej możemy powiedzieć, że jest to iloczyn liczby większej bądź równej 1 i mniejszej od 10 oraz dowolnej potęgi liczby 10.
Korzystając z poniższej planszy, zrób kilka przykładów z wykorzystaniem notacji wykładniczej.
Przejdź do planszy:
 http://jakzdacmaturezmatematyki.pl/plansze/dzialania-z-wykorzystaniem-notacji-wykladniczej-przyklady
http://jakzdacmaturezmatematyki.pl/plansze/dzialania-z-wykorzystaniem-notacji-wykladniczej-przykladyA teraz zrób zadania od 28 do 30 z książki (str. 30).
UŁAMKI OKRESOWE
Ostatnie zagadnienie na dzisiaj to ułamki okresowe. Przypomnij sobie najważniejsze pojęcia z tego tematu.
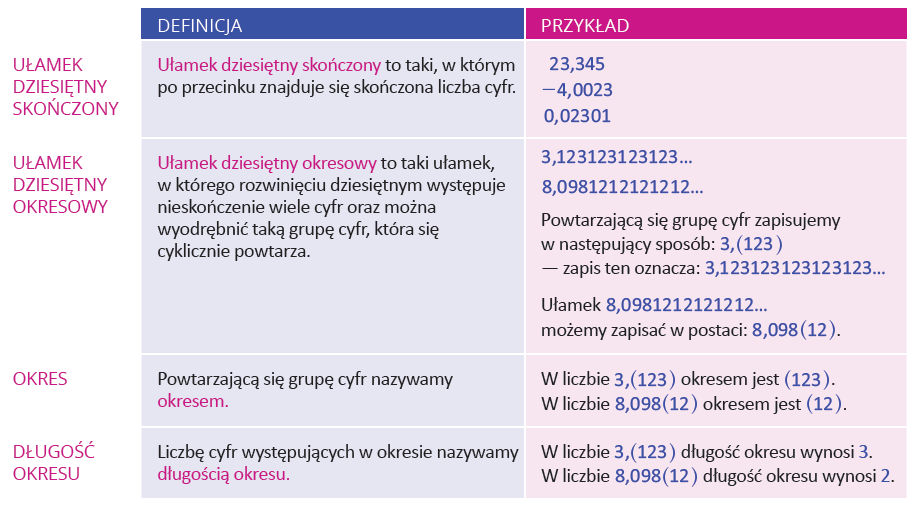
To, co musisz umieć, to ZAMIANA UŁAMKA OKRESOWEGO NA ZWYKŁY i ZAMIANA UŁAMKA ZWYKŁEGO NA OKRESOWY. W drugim przypadku, mając na maturze do dyspozycji kalkulator, możesz wykonać dzielenie i szybko uzyskać ułamek okresowy. Ale aby zamienić ułamek okresowy na zwykły, należy posłużyć się pewnym schematem.
Przypomnij sobie, jak to robimy, korzystając z planszy. Plansza jest dostępna w formie JPG, interaktywnej oraz VIDEO:
Przejdź do planszy:
 http://jakzdacmaturezmatematyki.pl/plansze/zamiana-ulamkow-okresowych-na-zwykle-przyklady
http://jakzdacmaturezmatematyki.pl/plansze/zamiana-ulamkow-okresowych-na-zwykle-przykladyOstatnie zadania z książki na dzisiaj to zadania od 31 do 33 (str. 32).
Dla przećwiczenia i utrwalenia wiadomości z dzisiejszego dnia test na zakończenie. Uda się zdobyć 100%?
POWODZENIA!

MATURA
2024
Z MATEMATYKI





 , 2014-02-28
, 2014-02-28