Mateusz I., 2013-05-11 
-
-
- INFORMATOR - ZAGADNIENIA
NIEOBOWIĄZUJĄCE NA MATURZE 2023 (liceum) - INFORMATOR - ZAGADNIENIA
NIEOBOWIĄZUJĄCE NA MATURZE 2023 (technikum) - DARMOWY PORADNIK O NAUCE
- PLANSZE I ZADANIA INTERAKTYWNE
- PEWNIAKI MATURALNE
- KSIĄŻKI ON-LINE
- TESTY ON-LINE
- MATURA Z MATEMATYKI 2024 ODPOWIEDZI
- ARKUSZE MATURALNE CKE
- TABLICE MATEMATYCZNE
- PODSTAWA PROGRAMOWA
- ZASADY MATURALNE - WAŻNE!
- KURS MATURALNY ON-LINE W FERIE
- WYPOŻYCZALNIA KSIĄŻEK ON-LINE
- ODBIERZ DARMOWĄ PŁYTĘ CD
- KURS EKSPRESOWY - INFORMACJE
- KURS EKSPRESOWY - ZAPISY
- WAŻNE INFORMACJE
- INFORMATOR - ZAGADNIENIA
-
SKLEPZAMÓWIENIA
GRUPOWE
Aby uzyskać przez szybką płatność DotPay dostęp do materiałów PREMIUM:
kliknij obok przycisk "dotpay" obok wybranej opcji i wykonaj szybką płatność.
kod dostępu zostanie wyświetlony po poprawnym zakończeniu transakcji i wysłany na podany adres e-mail.
Otrzymany kod wpisz w pole pod tabelką.
Aby uzyskać SMSem dostęp do materiałów PREMIUM:
wyślij krótki SMS na numer podany w tabeli obok wybranej opcji.
w zwrotnej widaomości sms otrzymasz kod dostępu do testów. Otrzymany kod wpisz w pole pod tabelką.
Usługa SMS dostępna w sieciach T-mobile, Plus, Play, Orange.Kod na 3 miesiące
koszt: 37,97 zł
(rabat 20%)47,46 złKod na pół roku
koszt: 49,97 zł
(rabat 20%)62,46 złPodane ceny usług są cenami brutto.
Właściciel serwisu:
Firma Edukacyjno-Wydawnicza ELITMAT Dariusz Kulma
ul. Okrzei 7
05-300 Mińsk Mazowiecki
elitmat@elitmat.pl
Usługi płatności internetowych obsługuje Eurokoncept, grupa Dotpay.
Regulamin Usług.
Reklamacja usługi Premium.
Lista plansz interaktywnych zawartych na płycie.1. Liczby rzeczywiste✔ Skracanie ułamków zwykłych - przykłady✔ Rozszerzanie ułamków zwykłych - przykłady do uzupełnienia✔ Zamiana ułamków mieszanych na ułamki niewłaściwe - przykłady✔ Zamiana ułamków niewłaściwych do postaci ułamków mieszanych - przykłady✔ Zamiana ułamków dziesiętnych na ułamki zwykłe - przykłady✔ Zamiana ułamków zwykłych na dziesiętne - przykłady✔ Zamiana ułamków okresowych na zwykłe - przykłady✔ Zamiana ułamka okresowego 1✔ Kolejność wykonywania działań✔ Podstawowe działania na ułamkach zwykłych niewłaściwych - przykłady✔ Działania łączne na ułamkach zwykłych - przykłady✔ Działania na ułamkach zwykłych i dziesiętnych - przykłady✔ Mnożenie liczb XY przez XZ gdzie Y+Z=10 np. 24x26✔ Pierwiastki dowolnego stopnia - przykłady z uzasadnieniem✔ Wyłączanie czynnika przed znak pierwiastka kwadratowego✔ Wyłączanie czynnika przed znak pierwiastka trzeciego stopnia✔ Włączanie czynnika pod znak pierwiastka kwadratowego✔ Włączanie czynnika pod znak pierwiastka trzeciego stopnia✔ Pierwiastki tego samego stopnia - wzory z przykładami✔ Działania na pierwiastkach - przykłady✔ Działania na pierwiastkach 2 - przykłady✔ Potęgi o wykładniku całkowitym ujemnym - przykłady✔ Własności potęg o tej samej podstawie - wzory z przykładami✔ Własności potęg o tym samym wykładniku - wzory z przykładami✔ Potęgi o wykładniku wymiernym - przykłady✔ Działania na potęgach o tym samym wykładniku✔ Działanie na potęgach 1✔ Działanie na potęgach 2✔ Notacja wykładnicza✔ Działania z wykorzystaniem notacji wykładniczej - przykłady✔ Odległości planet od Słońca z wykorzystaniem notacji wykładniczej✔ Obliczanie logarytmów z definicji - przykłady z uzasadnieniem✔ Logarytmy - najważniejsze wzory z przykładami✔ Obliczanie logarytmu z definicji z wykorzystaniem równania✔ Działanie - logarytmy - 2✔ Obliczanie logarytmów z definicji - zadanie z przykładami✔ Działanie - logarytmy - 5✔ Działanie - logarytmy - 6✔ Działanie - logarytmy - 3✔ Działanie - logarytmy✔ Przybliżenia ułamków dziesiętnych✔ Przybliżenia liczb - przykłady✔ Błąd bezwzględny✔ Błąd względny✔ Błąd względny 1✔ Błąd względny 2✔ Przybliżenia liczb - przykłady (java)✔ Przybliżenia ułamków dziesiętnych (java)✔ Wizualizacja przedziałów liczbowych ograniczonych i ich zapis✔ Wizualizacja przedziałów liczbowych nieograniczonych i ich zapis✔ Działania na przedziałach - przykłady✔ Ilustracja graficzna procentu jako wycinek koła✔ Jak skorzystać z proporcji prostej przy obliczaniu procentów?✔ Rodzaje obliczeń procentowych✔ Graficzne przedstawienie działań na zbiorach✔ Suma, różnica i część wspólna zbiorów - przykład✔ Zbiór liczb rzeczywistych i jego podzbiory✔ Cechy podzielności przez liczby 2, 3, 5, 9 - test z przykładami✔ Liczby pierwsze - sito Eratostenesa✔ Rozkład liczby na czynniki pierwsze - przykłady✔ Największy wspólny dzielnik (NWD) - przykłady✔ Najmniejsza wspólna wielokrotność (NWW) - przykłady✔ Edytor wyznaczania NWW i NWD dla liczb od 1 do 200✔ Wizualizacja wartości bezwzględnej na osi liczbowej✔ Wizualizacja wartości bezwzględnej2. Wyrażenia algebraiczne✔ Kwadrat sumy - zadanie z przykładami✔ Kwadrat sumy - wstęp✔ Kwadrat różnicy - zadanie z przykładami✔ Dowód geometryczny kwadratu sumy✔ Różnica kwadratów - zadanie z przykładami✔ Kwadrat różnicy - wstęp✔ Dowód geometryczny kwadratu różnicy✔ Różnica kwadratów - wstęp✔ Dowód geometryczny różnicy kwadratów✔ Szybkie obliczenia z wykorzystaniem wzorów skróconego mnożenia - przykłady✔ Uprość wyrażenia, korzystając ze wzorów skróconego mnożenia✔ Wyłączanie niewymierności z mianownika ułamka - przykłady✔ Dwumian Newtona a trójkąt Pascala✔ Wykazywanie, że liczba jest całkowita K1✔ Jak skorzystać z trójkąta Pascala✔ Wyłączanie niewymierności z mianownika ułamka 2 - przykłady✔ Wykazywanie, że liczba jest całkowita K2✔ Wykazywanie, że liczba jest całkowita K3✔ Wzory skróconego mnożenia drugiego stopnia✔ Wykazywanie, że liczba jest całkowita K4✔ Róźnica n-tej potęgi - zadanie 1✔ Róźnica n-tej potęgi - zadanie 2✔ Zadanie z wykorzystaniem wzorów skróconego mnoźenia - 7✔ Redukcja wyrazów podobnych - przykłady✔ Zapis słowny wyrażeń algebraicznych - przykłady✔ Mnożenie sum algebraicznych✔ Obliczanie wartości liczbowych wyrażeń algebraicznych - przykłady✔ Wyłącz wspólny czynnik poza nawias✔ Mnożenie i redukcja wyrażeń algebraicznych✔ Jak zapisywać dowody z podzielnością✔ Dowód z podzielnością K1✔ Wykaż, że suma trzech kolejnych liczb całkowitych jest podzielna przez 3✔ Dowód z podzielnością K2✔ Wykazywanie podzielności wyrażeń - przykłady✔ Dowód z podzielnością K3✔ Wykazywanie podzielności wyrażeń z wykorzystaniem wzorów skróconego mnożenia - przykłady✔ Dowód z podzielnością K4✔ Dowody z nierównościami - przykłady✔ Dowód z podzielnością K5✔ Dowód z podzielnością K6✔ Dowód z podzielnością K7✔ Dowód z podzielnością K8✔ Dowód z nierównością K1✔ Dowód z nierównością K2✔ Dowód z nierównością K33. Funkcje✔ Sprawdzanie czy dana liczba rzeczywista jest rozwiązaniem równania - przykłady✔ Sprawdzanie czy dana liczba rzeczywista jest rozwiązaniem nierówności - przykłady✔ Rozwiązywanie graficzne układu równań - przykłady✔ Interpretacja geometryczna układu równań - wstęp✔ Rozwiązywanie układu równań metodą wyznaczników✔ Rozwiązywanie układu równań metodą wyznaczników - wstęp✔ Działania na nierównościach - przykłady✔ Rodzaje nierówności liniowych - przykłady✔ Największa liczba całkowita spełniająca nierówność - zadanie✔ Równania kwadratowe - przykłady✔ Rodzaje równań kwadratowych✔ Zadanie tekstowe z równaniem kwadratowym 1✔ Zadanie tekstowe z równaniem kwadratowym 2✔ Zadanie tekstowe z równaniem kwadratowym 3✔ Zadanie tekstowe z równaniem kwadratowym 5✔ Zadanie tekstowe z równaniem kwadratowym 6✔ Zadanie tekstowe z równaniem kwadratowym 4✔ Zadanie tekstowe z równaniem kwadratowym 7✔ Nierówność kwadratowa - wstęp✔ Nierówność kwadratowa - przykłady 2✔ Nierówność z parametrem✔ Proste równania trzeciego stopnia - przykłady✔ Równania trzeciego stopnia - przykłady✔ Równania z wykorzystaniem równań stopnia trzeciego - przykłady✔ Równanie w postaci iloczynu 15✔ Równania w postaci iloczynu - zadanie✔ Równania w postaci iloczynu - przykłady✔ Rozwiązywanie równań trzeciego stopnia metodą grupowania✔ Równania wymierne równe zero - przykłady✔ Równania wymierne - przykłady✔ Zadanie tekstowe z równaniem wymiernym✔ Zadanie tekstowe - pompy✔ Działania na równaniach - przykłady✔ Rodzaje równań liniowych - przykłady✔ Równanie liniowe a liczba rozwiązań✔ Zadanie tekstowe z równaniem liniowym 1✔ Zadanie tekstowe z równaniem liniowym 2✔ Rozwiązywanie układu równań metodą podstawiania✔ Rozwiązywanie układu równań metodą przeciwnych współczynników✔ Zadanie tekstowe z układem równań 1✔ Zadanie tekstowe z układem równań 2✔ Skracanie ułamków algebraicznych - przykłady✔ Rozszerzanie ułamków algebraicznych - przykłady✔ Działania na wyrażeniach wymiernych - wstęp✔ Zadanie tekstowe - prędkość średnia 1✔ Zadanie tekstowe - Ojciec i syn rozładowują samochód4. Równania i nierówności✔ Sposoby opisywania funkcji✔ Określanie funkcji z wykresu - przykłady✔ Określanie funkcji z grafu - przykłady✔ Wyznaczanie dziedziny funkcji określonej za pomocą wzoru✔ Funkcja - opis słowny✔ Przesunięcie wykresu funkcji kwadratowej wzdłuż osi OX i OY - postać kanoniczna✔ Obliczanie współrzędnych wierzchołka paraboli - przyklady✔ Zamiana postaci ogólnej funkcji kwadratowej na postać kanoniczną✔ Ilość miejsc zerowych funkcji kwadratowej w zależności od delty✔ Obliczanie miejsc zerowych funkcji kwadratowej z wykorzystaniem wzorów✔ Zamiana postaci ogólnej funkcji kwadratowej na postać iloczynową✔ Ilość miejsc zerowych w zależności od delty - zadanie z przykładami✔ Szkicowanie wykresu funkcji kwadratowej✔ Obliczanie miejsc zerowych - zadanie z przykładami✔ Własności funkcji kwadratowej na podstawie wykresu - przykłady✔ Wierzchołek paraboli✔ Funkcja kwadratowa - obliczanie współczynników✔ Funkcja kwadratowa - obliczanie współczynników 2✔ Największa i najmniejsza wartość funkcji kwadratowej w przedziale✔ Największa i najmniejsza wartość funkcji kwadratowej w przedziale - zadanie z przykładami✔ Własności funkcji - zadanie praktyczne 1✔ Własności funkcji - zadanie praktyczne 2✔ Szkicowanie hiperboli - przykłady✔ Wykres hiperboli✔ Proporcjonalność odwrotna✔ Jak rozwiązywać zadania z proporcjonalnością odwrotną - przykłady✔ Proporcjonalność odwrotna 1✔ Szkicowanie funkcji wykładniczej - przykłady✔ Funkcja wykładnicza✔ Funkcja wykładnicza - zadanie praktyczne 1✔ Odczytywanie wartości funkcji dla danego argumentu✔ Odczytywanie argumentu funkcji dla danej wartości✔ Obliczanie wartości funkcji gdy dany jest argument✔ Odczytywanie z wykresu wartości funkcji dla danego argumentu✔ Podstawowe własności funkcji - zadanie z przykładami✔ Podstawowe własności funkcji✔ Własności funkcji - zadanie 1✔ Własności funkcji - zadanie 2✔ Własności funkcji - zadanie 3✔ Własności funkcji - zadanie 4✔ Przesunięcie równoległe funkcji - wstęp 1✔ Przesunięcie równoległe funkcji - zadanie z przykładami✔ Przekształcenia wykresu funkcji względem osi układu współrzędnych✔ Przesunięcie równoległe funkcji - zadanie z przykładami 2✔ Przekształcenia wykresu funkcji względem osi OX - zadanie z przykładami✔ Przekształcenia wykresu funkcji względem osi OY - zadanie z przykładami✔ Rysowanie funkcji liniowej - tabelka✔ Jak narysować funkcję liniową✔ Jak szybko narysować funkcję liniową✔ Znajdowanie wzoru funkcji przechodzącej przez dwa punkty - przykłady✔ Znajdowanie wzoru funkcji liniowej na podstawie wykresu✔ Współczynniki funkcji liniowej✔ Współczynniki funkcji liniowej a ćwiartki układu współrzędnych - zadanie z przykładami✔ Funkcja liniowa i jej własności - zadanie z przykładami✔ Współczynniki funkcji kwadratowej - przykłady✔ Wykres funkcji f(x)=ax^2, gdzie a jest dodatnie✔ Wykres funkcji f(x)=ax^2, gdzie a jest ujemne✔ Znajdowanie wzoru funkcji kwadratowej przechodzącej przez trzy punkty✔ Proporcjonalność prosta - przykłady✔ Jak rozwiązywać zadania z proporcjonalnością prostą - przykłady✔ Wykres hiperboli 2✔ Wykres hiperboli 15. Ciągi✔ Przykłady ciągów - wzór i wykres✔ Wyrazy ciągu - przykłady✔ Wykresy ciągów opisanych wzorem - przykłady✔ Wyznaczanie numeru wyrazu dla danej wartości - przykłady✔ Wyznaczanie liczby wyrazów ciągu spełniających określone warunki - zadanie 3✔ Obliczanie wyrazu ciągu - zadanie✔ Monotoniczność ciągów - przykłady✔ Badanie monotoniczności ciągu - zadanie 1✔ Graficzna interpretacja ciągu Fibonacciego✔ Odczytywanie pierwszego wyrazu i różnicy ciągu arytmetycznego z wykresu - przykłady✔ Wyznaczanie najważniejszych parametrów ciągu arytmetycznego - zadanie 2✔ Wykazywanie, że ciąg jest arytmetyczny✔ Wyznaczanie wzoru ogólnego ciągu arytmetycznego - zadanie 1✔ Ciąg arytmetyczny - obliczanie wyrazów ciągu 1✔ Wyznaczanie najważniejszych parametrów ciągu arytmetycznego - zadanie 1✔ Obliczanie różnicy i pierwszego wyrazu ciągu arytmetycznego, gdy dane są dwa wyrazy - przykłady✔ Ciąg arytmetyczny - obliczanie wyrazów ciągu 2✔ Obliczanie brakujących wyrazów ciągu arytmetycznego - przykłady✔ Ciąg arytmetyczny - obliczanie wyrazów ciągu (dwie niewiadome) 1✔ Wykazywanie, że ciąg jest arytmetyczny dla każdego parametru✔ Odczytywanie pierwszego wyrazu i ilorazu ciągu geometrycznego z wykresu - przykłady✔ Wyznaczanie najważniejszych parametrów ciągu geometrycznego - zadanie 2✔ Wykazywanie, że ciąg jest geometryczny✔ Wyznaczanie najważniejszych parametrów ciągu geometrycznego - zadanie 3✔ Wyznaczanie najważniejszych parametrów ciągu geometrycznego - zadanie 1✔ Obliczanie wyrazów ciągu geometrycznego - zadanie 1✔ Obliczanie ilorazu i pierwszego wyrazu ciągu geometrycznego, gdy dane są dwa wyrazy✔ Obliczanie brakujących wyrazów ciągu geometrycznego - przykłady✔ Obliczanie wyrazów ciągu geometrycznego - zadanie 2 (wersja \"a\")✔ Obliczanie sumy n początkowych wyrazów ciągu arytmetycznego - przykłady✔ Wykorzystanie wzoru na sumę n początkowych wyrazów ciągu arytmetycznego - zadanie 1✔ Wykorzystanie wzoru na sumę n początkowych wyrazów ciągu arytmetycznego - zadanie 2✔ Zależność między sumą S_n a wyrazami ciągu a_n - dowód✔ Wykorzystanie zależności ciągu arytmetycznego do obliczania kątów czworokąta - zadanie✔ Wyznaczanie wzoru ogólnego ciągu za pomocą wzoru na sumę - zadanie✔ Wykazywanie, że ciąg jest arytmetyczny, gdy dany jest wzór na sumę✔ Obliczanie sumy n początkowych wyrazów ciągu geometrycznego - przykłady✔ Wykorzystanie wzoru na sumę n początkowych wyrazów ciągu geometrycznego - zadanie 16. Trygonometria✔ Funkcje trygonometryczne - wstęp✔ Funkcje trygonometryczne w trójkącie✔ Odczytywanie funkcji trygonometrycznych w trójkącie - przykłady✔ Działania z wykorzystaniem wartości funkcji trygonometrycznych dla kątów mniejszych niż 90 stopni - przykłady✔ Obliczanie funkcji trygonometrycznych w trójkącie - przykłady✔ Wartości funkcji trygonometrycznych - uzupełnianka✔ Działania z wykorzystaniem wartości funkcji trygonometrycznych dla kątów większych od 90 stopni a mniejszych niż 180 stopni - przykłady✔ Wyznaczanie kątów za pomocą funkcji trygonometrycznych - przykłady✔ Wartości funkcji trygonometrycznych z przedziału 90 -180 stopni✔ Tablice trygonometryczne✔ Odczytywanie wartości z tablic trygonometrycznych - przykłady✔ Zadanie praktyczne z wykorzystaniem funkcji trygonometrycznych✔ Wyprowadzenie wzoru na jedynkę trygonometryczną✔ Wykorzystanie zależności trygonometrycznych - przykłady✔ Zadanie na wykorzystanie własności trygonometrycznych 1✔ Zadanie na wykorzystanie własności trygonometrycznych 2✔ Tożsamość trygonometryczna 4✔ Tożsamość trygonometryczna 3✔ Wyznaczanie wartości pozostałych funkcji trygonometrycznych, gdy podany jest sinus lub cosinus - wstęp✔ Wyznaczanie pozostałych wartości funkcji trygonometrycznych z wykorzystaniem wzorów - przykłady✔ Obliczanie wartości pozostałych funkcji trygonometrycznych - przykłady✔ Obliczanie wartości trygonometrycznych - zadanie✔ Trójki pitagorejskie - test✔ Obliczanie wartości pozostałych funkcji trygonometrycznych 2 - przykłady✔ Trójkąty pitagorejskie - znajdowanie brakującej długości boku✔ Obliczanie wartości funkcji trygonometrycznych dla kątów większych od 90 stopni✔ Obliczanie wartości funkcji trygonometrycznych dla kątów większych od 90 stopni, a mniejszych niż 180 stopni✔ Zależność między sinusem i cosinusem✔ Określanie funkcji trygonometrycznych w trójkącie - 3 przykłady✔ Obliczanie pozostałych funkcji trygonometrycznych gdy dany jest cosinus✔ Działanie z wartościami funkcji trygonometrycznych dla kątów większych niż 90 stopni✔ Obliczanie pozostałych funkcji trygonometrycznych gdy dany jest sinus✔ Obliczanie pozostałych funkcji trygonometrycznych gdy dany jest tangens7. Planimetria✔ Podstawowe wiadomości o kole i okręgu✔ Kąty środkowe - przykład✔ Kąty środkowy i wpisany oparte na tym samym łuku - zadanie 2✔ Obliczanie kąta środkowego, gdy dana jest długość łuku✔ Kąt środkowy i wpisany oparte na tym samym łuku okręgu✔ Kąty środkowe i wpisane oparte na tym samym łuku - przykłady✔ Obliczanie kąta wpisanego, gdy dana jest długość łuku✔ Kąt środkowy i wpisany oparte na tym samym łuku - zadanie 5✔ Kąty środkowy i wpisany oparte na tym samym łuku - zadanie 1✔ Kąt środkowy i wpisany oparte na tym samym łuku - zadanie 4✔ Kąt środkowy i wpisany oparte na tym samym łuku - zadanie 3✔ Kąty środkowy i wpisany oparte na tym samym łuku - zadanie 6✔ Twierdzenie o kątach wpisanych opartych na średnicy okręgu✔ Dowód geometryczny z wykorzystaniem kątów wpisanych✔ Twierdzenie o kątach wpisanych opartych na tym samym łuku.✔ Twierdzenie o kątach środkowych opartych na tych samych łukach✔ Wzajemne położenie prostej i okręgu✔ Twierdzenie o kącie między styczną i cięciwą✔ Okrąg i styczna - zadanie✔ Okrąg i styczna - przykłady✔ Wzajemne położenie dwóch okręgów✔ Wzajemne położenie dwóch okręgów - przykłady✔ Cechy podobieństwa trójkątów✔ Trójkąty podobne - zadanie 1✔ Trójkąty podobne - zadanie 2✔ Trójkąty podobne - zadanie 3✔ Trójkąty podobne - zadanie 4✔ Pole trójkąta, gdy dany jest kąt i dwa boki - przykłady✔ Pole równoległoboku, gdy dany jest kąt i dwa boki - przykłady✔ Pole rombu, gdy dany jest bok i kąt - przykłady✔ Planimetria - zadanie 3✔ Dowód geometryczny - kąty 1✔ Dowód geometryczny - kąty 2✔ Rodzaje kątów✔ Kąty przyległe✔ Kąty wierzchołkowe✔ Kąty odpowiadające✔ Kąty naprzemianległe✔ Suma kątów w trójkącie✔ Suma kątów w czworokącie✔ Wielokąty i ich podstawowe własności✔ Kąty w trójkącie - zadanie✔ Wielokąt foremny - zadanie✔ Rodzaje czworokątów - podstawowe wzory na pola i obwody✔ Planimetria - zadanie 1✔ Planimetria - zadanie 2✔ Ważne odcinki w wielokątach - środkowa, symetralna, dwusieczna, wysokość✔ Dowód twierdzenia Pitagorasa✔ Trójkąt o kątach 30,60,90 stopni✔ Trójkąt o kątach 45, 45, 90 stopni✔ Planimetria - zadanie 4✔ Okrąg opisany na wielokącie✔ Okrąg opisany na trójkącie✔ Okrąg wpisany w wielokąt✔ Okrąg wpisany w trójkąt✔ Trójkąt równoboczny - ważne wzory✔ Trójkąt prostokątny - ważne wzory✔ Kąty w trójkącie - zadanie 1✔ Kwadrat wpisany w okrąg - zadanie✔ Trójkąt prostokątny wpisany w okrąg - zadanie✔ Trójkąt prostokątny opisany na okręgu - zadanie✔ Promień okręgu wpisanego w trójkąt równoboczny - zadanie✔ Sześciokąt foremny opisany na okręgu - zadanie✔ Czworokąt wpisany w okrąg - zadanie✔ Twierdzenie o okręgu opisanym na czworokącie✔ Twierdzenie o czworokącie opisanym na okręgu✔ Trójkąty przystające - przykłady✔ Trójkąty przystające - dowód geometryczny 1✔ Trójkąty przystające - dowód geometryczny 2✔ Trójkąty przystające - dowód geometryczny 3✔ Twierdzenie Talesa✔ Twierdzenie Talesa - zadanie✔ Podział odcinka na trzy równe części - zadanie✔ Twierdzenie Talesa - przykłady✔ Figury podobne - przykłady✔ Figury podobne - skala✔ Wielokąty podobne - zadanie✔ Wielokąty podobne - zadanie 2✔ Dowód geometryczny - matura 23.11.2016✔ Planimetria - Kąty w trójkącie8. Geometria na płaszczyźnie kartezjańskiej✔ Zamiana równania prostej z postaci kierunkowej na postać ogólną - przykłady✔ Zamiana równania prostej z postaci ogólnej na postać kierunkową - przykłady✔ Wyznaczanie wzoru prostej przechodzącej przez dwa punkty za pomocą układu równań✔ Obliczanie współczynnika kierunkowego - przykłady✔ Wyznaczanie wzoru prostej przechodzącej przez dwa punkty - przykłady✔ Równanie okręgu w postaci ogólnej - przykłady✔ Równanie okręgu w postaci kanonicznej - przykłady✔ Prosta równoległa do danej przechodząca przez wybrany punkt✔ Badanie równoległości funkcji - test✔ Prosta prostopadła do danej przechodząca przez wybrany punkt✔ Badanie prostopadłości funkcji - test✔ Proste prostopadłe - wyznaczanie wartości parametru✔ Wyznaczanie prostej równoległej do danej✔ Wyznaczanie prostej prostopadłej do danej✔ Wyznaczanie punktu przecięcia dwóch prostych✔ Wyznaczanie punktu przecięcia dwóch prostych 2✔ Pole trójkąta w układzie współrzędnych - zadanie✔ Trójkąt w układzie współrzędnych - zadanie✔ Środek odcinka w układzie współrzędnych✔ Zadanie z wykorzystaniem wzoru na środek odcinka - przykład 2✔ Zadanie z wykorzystaniem wzoru na środek odcinka - przykład 1✔ Znajdowanie wzoru symetralnej odcinka 1✔ Znajdowanie wzoru symetralnej odcinka 2✔ Znajdowanie wzoru symetralnej odcinka 4✔ Obwód trójkąta równobocznego - zadanie✔ Długość odcinka w układzie współrzędnych - przykłady✔ Pole kwadratu - zadanie 1✔ Obwód rombu - zadanie✔ Trójkąt równoramienny - zadanie✔ Odległość punktu od prostej - przykłady✔ Pole trójkąta - zadanie✔ Obliczanie pola trójkąta w układzie współrzędnych bezpośrednio ze wzoru✔ Pole trójkąta - zadanie 2✔ Pole równoległoboku - zadanie✔ Obraz trójkąta w symetrii osiowej✔ Obraz punktu w symetrii osiowej względem osi układu współrzędnych✔ Symetrie trójkąta - zadanie✔ Obraz czworokąta w symetrii środkowej✔ Symetrie czworokąta - zadanie✔ Obraz punktu w symetrii środkowej względem początku układu współrzędnych✔ Symetrie kwadratu - zadanie✔ Obrazy figur w symetriach osiowej lub środkowej w układzie współrzędnych - przykłady9. Stereometria✔ Wzajemne położenie dwóch płaszczyzn - 1✔ Wzajemne położenie prostej i płaszczyzny✔ Rozpoznawanie krawędzi prostopadłych i równoległych - przykłady✔ Przekątne graniastosłupa - zadanie✔ Graniastosłupy proste - wstęp✔ Graniastosłupy pochyłe - wstęp✔ Graniastosłupy prawidłowe n-kątne✔ Ostrosłupy - wstęp✔ Czworościan foremny - siatka✔ Sześcian - siatka✔ Ośmiościan foremny - siatka✔ Dwunastościan foremny - siatka✔ Dwudziestościan foremny - siatka✔ Ostrosłup prawidłowy trójkątny - kąty między odcinkami✔ Ostrosłup prawidłowy czworokątny - kąty między odcinkami✔ Graniastosłup prawidłowy trójkątny - kąty między odcinkami✔ Graniastosłup prawidłowy czworokątny - kąty między odcinkami✔ Kąty w ostrosłupie - przykłady✔ Ostrosłup prawidłowy trójkątny - kąty miedzy odcinkami i płaszczyznami✔ Ostrosłup prawidłowy czworokątny - kąty między odcinkami i płaszczyznami✔ Graniastosłup prawidłowy trójkątny - kąty między odcinkami i płaszczyznami✔ Graniastosłup prawidłowy czworokątny - kąty między odcinkami i płaszczyznami✔ Kąty w prostopadłościanie - przykłady✔ Graniastosłup prawidłowy trójkątny - zadanie✔ Walec✔ Jak powstaje walec✔ Walec- siatka✔ Jak narysować walec✔ Stożek✔ Jak powstaje stożek✔ Stożek - siatka✔ Jak narysować stożek✔ Jak powstaje kula✔ Obliczanie tworzącej stożka - przykłady✔ Kąt dwuścienny✔ Ostrosłup prawidłowy czworokątny - zadanie✔ Graniastosłup prawidłowy trójkątny (przekrój) - zadanie 1✔ Przekroje prostopadłościanu✔ Przekrój prostopadłościanu - zadanie 1✔ Przekroje sześcianu✔ Przekroje sześcianu 2✔ Graniastosłup prawidłowy trójkątny (przekrój) - zadanie 2✔ Przekroje sześcianu - przykłady✔ Przekrój prostopadłościanu - przykłady✔ Sześcian - zadanie 1✔ Objętość - wizualizacja✔ Sześcian - zadanie 2✔ Prostopadłościan - najważniejsze wzory✔ Sześcian - zadanie 3✔ Prostopadłościan - siatka✔ Sześcian - zadanie 4✔ Sześcian - najważniejsze wzory✔ Wszystkie rodzaje siatek sześcianu✔ Prostopadłościan - zadanie 1✔ Sześcian - rodzaje zadań✔ Prostopadłościan - zadanie 2✔ Prostopadłościan - rodzaje zadań✔ Prostopadłościan - zadanie 3✔ Graniastosłup prawidłowy trójkątny✔ Graniastosłup prawidłowy trojkątny - siatka✔ Jak narysować graniastosłup trójkątny✔ Graniastosłup prawidłowy czworokątny✔ Graniastosłup prawidłowy czworokątny - siatka✔ Jak narysować graniastosłup czworokątny✔ Graniastosłup prawidłowy sześciokątny✔ Graniastosłup prawidłowy sześciokątny - siatka✔ Jak narysować graniastosłup sześciokątny✔ Graniastosłup prawidłowy trójkątny - rodzaje zadań✔ Graniastosłup prawidłowy czworokątny - rodzaje zadań✔ Graniastosłup prawidłowy trójkątny - zadanie 5✔ Graniastosłup o podstawie prostokąta - zadanie✔ Zależność między objętością ostrosłupa i graniastosłupa - wizualizacja✔ Czworościan foremny - najważniejsze wzory✔ Jak narysować czworościan✔ Sześcian ścięty do ostrosłupa - zadanie✔ Ostrosłup prawidłowy trójkątny✔ Ostrosłup prawidłowy trójkątny - siatka✔ Ostrosłup czworokątny o podstawie prostokąta - zadanie✔ Jak narysować ostrosłup trójkątny✔ Ostrosłup prawidłowy czworokątny✔ Ostrosłup prawidłowy czworokątny - siatka✔ Jak narysować ostrosłup czworokątny✔ Ostrosłup prawidłowy sześciokątny✔ Ostrosłup prawidłowy sześciokątny - siatka✔ Jak narysować ostrosłup sześciokątny✔ Czworościan foremny - przykłady✔ Graniastosłup ścięty do ostrosłupa - zadanie✔ Ostrosłup prawidłowy czworokątny - zadanie✔ Stożek - zadanie✔ Zależność między objętością stożka i walca - wizualizacja✔ Walec - zadanie✔ Walec - przykłady✔ Kula - zadanie✔ Stożek - przykłady✔ Kula - przykłady✔ Kula - zadanie z przekrojem10. Elementy statystyki opisowej. Teoria prawdopodobieństwa i kombinatoryka✔ Kombinatoryka - przykłady✔ Kombinatoryka 25✔ Kombinatoryka - przykłady 2✔ Kombinatoryka - przykłady 3✔ Kombinatoryka - przykłady 4✔ Wstęp do prawdopodobieństwa - przykłady✔ Wstęp do prawdopodobieństwa - przykłady 2✔ Podwójny rzut kostką - przykłady✔ Prawdopodobieństwo - zadanie 1✔ Diagram z wynikami losowymi rzutu dwoma kostkami✔ Prawdopodobieństwo - zadanie 3✔ Podwójny rzut kostką - zadanie 1✔ Podwójny rzut kostką - zadanie 2✔ Prawdopodobieństwo - zadanie 2✔ Prawdopodobieństwo - zadanie 4✔ Średnia arytmetyczna - przykłady✔ Średnia arytmetyczna z danymi z diagramu - przykłady✔ Średnia arytmetyczna - obliczanie brakującego elementu - przykłady✔ Mediana - przykłady
Wykup najdłuższy dostęp do STREFY PREMIUM i odbierz ZA DARMO płytę CD zawierająca 500 plansz interaktywnych (o wartości 49 zł).Plansze zawierają zagadnienia teoretyczne i rozwiązania zadań "krok po kroku" z zakresu przygotowania do matury. Rozwiązania "krok po kroku" to świetny sposób na naukę:
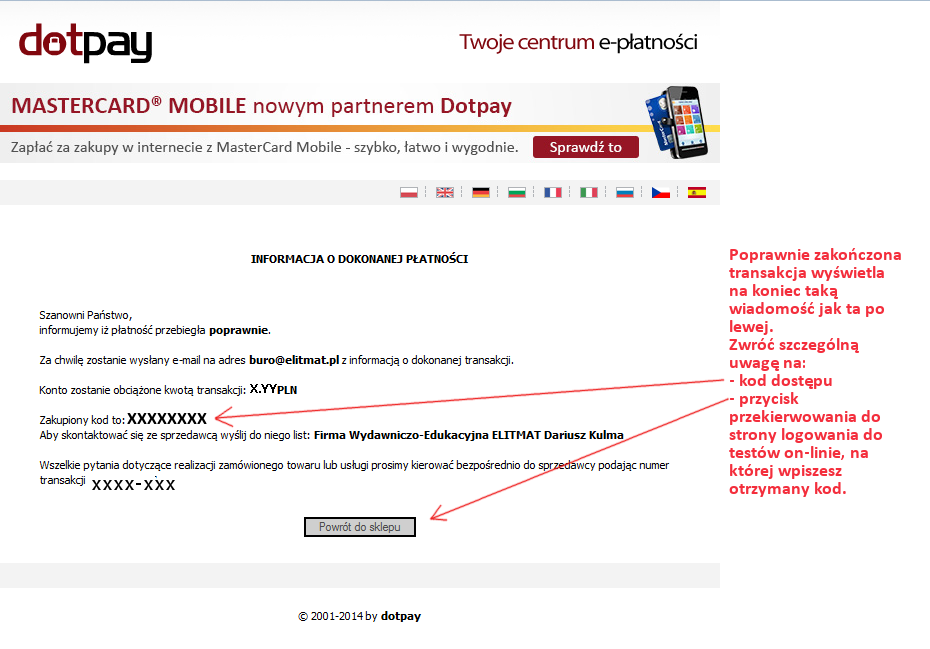
na początku wyświetlana jest treść zadania, którą możesz przeanalizować.
następnie możesz wyświetlać kolejne etapy rozwiązywania zadania - każdy etap to obliczenia + komentarz.
każdy krok możesz przejść w dowolnym tempie, możesz też wyświetlić od razu całe rozwiązanie.
to doskonały sposób na samodzielną naukę przed maturą lub sprawdzianem!
🔍 Zobacz listę plansz zawartych na tej płycieZobacz jak wyglądają plansze interaktywne
Ważne dla nauczycieli:Plansze z płyty doskonale nadają się do wyświetlania na tablicach interaktywnych! Dzięki nim możesz usprawnić swoją pracę w klasie.
Płyta zawiera 500 plansz interaktywnych, znaczna część plansz zawiera co najmniej kilka przykładów dla danego typu zadań - to ogromna baza zadań maturalnych! Dużo większa niż w większości repetytoriów maturalnych - dodatkowo każde zadanie posiada pełne rozwiązanie "krok po kroku", a nie tylko odpowiedź!Według różnych badań ponad połowa osób posiada pamięć wzrokową (niekt. źródła podają nawet 85%)To znaczy, że łatwiej im się uczyć jeżeli materiały są dobrze i wyraźnie pokolorowane. Wszystkie plansze na płycie są dostosowane do tej zasady - poszczególne elementy są tak pokolorowane, aby ułatwić uczenie i poprawić zapamiętywanie!
Tylko teraz, z okazji premiery płyty, możesz ją mieć zupełnie za darmo!
Aby odebrać darmowy egzemplarz płyty, wypełnij formularz na > tej < stronie i wpisz wykupiony kod. Płytę wyślemy przesyłką priorytetową!
Ilość egzemplarzy promocyjnych ograniczona!
To jest tylko podgląd zadań. Aby rozwiązać maturę wybierz opcję:
✖
MATURA PRÓBNA
MINI-MATURA POZIOM PODSTAWOWY.
Czas pracy: 170 minut .
Zadania rozwiązuj na kartce, następnie zaznaczaj odpowiedzi aby sprawdzić swój wynik.
TWÓJ CZAS:170:00 ZADANIE nr 1. (1 pkt.) Na lokatę trzymiesięczną o oprocentowaniu rocznym równym\[3\% \]wpłacono\[8500 \]zł. Po zakończeniu lokaty wartość odsetek wynosi:Wybierz odpowiedź:
ZADANIE nr 2. (1 pkt.) Dane są liczby\[a=\log_4 \frac{1}{2},\;b=\log_8 2,\; c= \log_2 \frac{1}{4}\]. Prawdą jest, że:Wybierz odpowiedź:
ZADANIE nr 3. (1 pkt.) Liczba\[16^{-\frac34}\]jest równa:Wybierz odpowiedź:ZADANIE nr 4. (1 pkt.) Wyrażenie\[(2x+y+1)^2 \]jest równe:Wybierz odpowiedź:ZADANIE nr 5. (1 pkt.) Odległość z miasta\[X\]do miasta\[Y\]samochód, który jedzie ze średnią prędkością\[80\; \frac{ \mathrm{km}}{ \mathrm{h}}\], pokonuje w pół godziny. Jeżeli samochód zwiększy swoją średnią prędkość do\[120\; \frac{ \mathrm{km}}{ \mathrm{h}}\], to czas przejazdu na tej samej trasie skróci się o:Wybierz odpowiedź:ZADANIE nr 6. (1 pkt.) Funkcja\[ f \], określona dla wszystkich liczb naturalnych, przyporządkowuje każdej liczbie ostatnią cyfrę jej dwukrotności. Zbiór wartości funkcji zawiera dokładnie:Wybierz odpowiedź:ZADANIE nr 7. (1 pkt.) Funkcje\[f(x)=2^{x}\]i\[g(x) = \left(\frac{1}{2} \right)^{x}\]są:Wybierz odpowiedź:ZADANIE nr 8. (1 pkt.) Zbiorem rozwiązań nierówności\[\frac{3-x}{2}-\frac{x}{3} < x\]jest przedział:Wybierz odpowiedź:ZADANIE nr 9. (1 pkt.) Iloczyn wszystkich pierwiastków równania\[(x^2-2)(x^3-8)(x^2-8)(x^2+9) =0 \]jest równy:Wybierz odpowiedź:ZADANIE nr 10. (1 pkt.) W zadaniach 8. i 9. wykorzystaj przedstawiony poniżej wykres funkcji\[f(x)\].
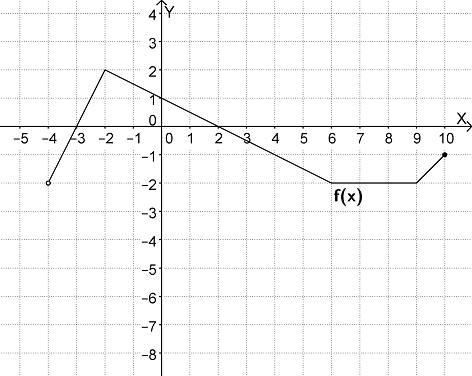
Czy Twój wynik jest zgodny z podanym rozwiązaniem?:
ZADANIE nr 11. (1 pkt.) Funkcję\[f(x)\]przekształcono i otrzymano funkcję\[g(x)=f(x)+2\]. Funkcja\[g(x)\]:Wybierz odpowiedź:ZADANIE nr 12. (1 pkt.) Janek składa na pół prostokątną kartkę papieru o grubości\[0,1\]mm. Po pierwszym złożeniu czynność powtarza, składając kartkę w ten sam sposób, i otrzymuje coraz mniejsze, ale zarazem coraz grubsze prostokąty. Po siedmiu złożeniach kartki Janka grubość papieru będzie wynosiła:Wybierz odpowiedź:ZADANIE nr 13. (1 pkt.) W ciągu arytmetycznym\[(a_n)\]dane są wyrazy\[a_{2017}=2016\]i\[a_{2015}=2017\]. Wzór ogólny tego ciągu ma postać:Wybierz odpowiedź:ZADANIE nr 14. (1 pkt.) Liczba\[ \frac{(\sin 120^{\circ})^2}{\cos 135 ^{\circ}}\]jest równa:Wybierz odpowiedź:ZADANIE nr 15. (1 pkt.) W trójkącie, który jest przedstawiony na rysunku poniżej, cosinus kąta ostrego\[\alpha\]jest równy: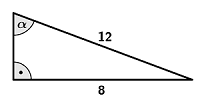
Wybierz odpowiedź:ZADANIE nr 16. (1 pkt.) Dany jest sześciokąt foremny, którego krótsza przekątna ma długość\[4\sqrt3 \]. Pole tego sześciokąta jest równe:Wybierz odpowiedź:ZADANIE nr 17. (1 pkt.) Dany jest trapez równoramienny (zobacz rysunek), w którym\[|BC|=|AD|=|DC|=29\], a wysokość trapezu jest równa\[21\]. Długość\[|AB|\]wynosi:
Wybierz odpowiedź:ZADANIE nr 18. (1 pkt.) Dany jest okrąg o środku\[O\], w który wpisano trójkąt\[ABC\](zobacz rysunek). Miara kąta\[\alpha\]wynosi:
Wybierz odpowiedź:ZADANIE nr 19. (1 pkt.) Dane są proste:\[p:\; y=(m^2+2)x-m\]oraz\[q:\;y=-\frac{3}{4}x+m\]. Prawdą jest, że istnieje taki parametr\[m\], dla którego proste:Wybierz odpowiedź:ZADANIE nr 20. (1 pkt.) Dany jest trójkąt zawarty między prostymi\[k,\;l\]oraz osią\[OY\], gdzie:\[k:\;y=-x+2\]i\[l:\;y=x-4\]. Pole tego trójkąta jest równe:Wybierz odpowiedź:ZADANIE nr 21. (1 pkt.) Dany jest ostrosłup czworokątny o podstawie prostokąta (zobacz rysunek). Korzystając z danych na rysunku, można stwierdzić, że kąt\[\alpha\]ma miarę: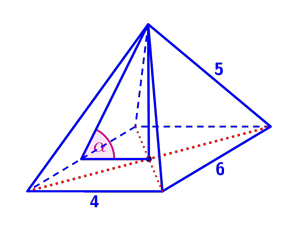
Wybierz odpowiedź:ZADANIE nr 22. (1 pkt.) Tworząca stożka jest o\[10\]dłuższa od jego wysokości, a obwód podstawy stożka wynosi\[60 \pi \]. Długość wysokości tego stożka jest więc równa:Wybierz odpowiedź:ZADANIE nr 23. (1 pkt.) Liczb czterocyfrowych o wszystkich cyfrach parzystych jest:Wybierz odpowiedź:ZADANIE nr 24. (1 pkt.) Rzucamy czterokrotnie symetryczną monetą. Prawdopodobieństwo, że wypadną co najmniej\[3\]orły, jest równe:Wybierz odpowiedź:ZADANIE nr 25. (1 pkt.) W tabeli zebrano informacje dotyczące liczby osób w rodzinach uczniów klasy III A. Średnia liczba osób w rodzinie dla uczniów tej klasy jest równa\[3,8\]. Wtedy liczba\[x\]jest równa:
Wybierz odpowiedź:ZADANIE nr 26. (1 pkt.) Mediana uporządkowanego niemalejącego zestawu sześciu liczb:\[2,\;3,\;4,\;x,\;7,\;8 \]jest równa\[4\]. Wtedy:Wybierz odpowiedź:ZADANIE nr 27. (2 pkt.) Rozwiąż nierówność\[10 x \le 3(x^2+1)\].\[x\in\left(-\infty;\;\frac13\right\rangle\cup\langle3;\;\infty)\]\[x\in\left(-\infty;\;-\frac13\right\rangle\cup\langle3;\;\infty)\]\[x\in\left(-\infty;\;-3\right\rangle\cup\left\langle\frac13;\;\infty\right)\]\[x\in\left(-\infty;\;-3\right\rangle\cup\left\langle-\frac13;\;\infty\right)\]\[\left\langle\frac13;\;3\right\rangle\]
Przeciągnij poprawne rozwiązanie w to pole:ZADANIE nr 28. (2 pkt.) Wykaż, że jednym z rozwiązań równania\[\frac{4x-5}{2x-2,5} = \frac{2x}{7}\]jest liczba pierwsza.Podaj odpowiedzi:
Rozwiązaniem równania jest liczba pierwsza równa (2 pkt.)ZADANIE nr 29. (2 pkt.) Liczby\[5,\;x,\;y \]w podanej kolejności tworzą rosnący ciąg geometryczny, przy czym\[ y-x=10 \]. Oblicz\[x\]i\[y\].Podaj odpowiedzi:
\[x= \](1 pkt.)
\[y= \](1 pkt.)ZADANIE nr 30. (2 pkt.) Wykaż, że liczba\[ \frac{\sqrt{103}+\sqrt{101}}{\sqrt{103}- \sqrt{101}}+\frac{\sqrt{103}-\sqrt{101}}{\sqrt{103}+ \sqrt{101}}\]jest liczbą naturalną.Podaj odpowiedzi:
Wykazałem, że podana liczba jest liczbą naturalną równą (2 pkt.)
ZADANIE nr 31. (2 pkt.) Dane są proste o równaniach\[p:\; y=2x,\;r:\;y=-x+6\]i\[q:\; y=(a+1)x+2a\]. Określ, dla jakiego parametru\[a\]proste te przecinają się w jednym punkcie.Podaj odpowiedzi:
\[a= \](2 pkt.)ZADANIE nr 32. (2 pkt.) Na bokach trójkąta równobocznego\[ABC\]leżą punkty\[ K,\;L,\;M\]w taki sposób, że punkt\[K\]leży na boku\[AB\], punkt\[L\]leży na boku\[BC\], a punkt\[M\]leży na boku\[AC\]oraz zachodzi równość\[|AK|=|BL|=|CM| \](zobacz rysunek). Wykaż, że trójkąt\[KLM\]jest równoboczny.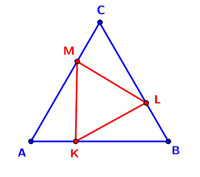
Wybierz odpowiedź:ZADANIE nr 33. (4 pkt.) Tworząca stożka jest o\[3\]dłuższa od średnicy jego podstawy. Wiedząc, że wysokość stożka jest\[12\], oblicz jego pole powierzchni całkowitej oraz objętość.Podaj odpowiedzi:
Tworząca stożka jest równa (1 pkt.)
Objętość stożka jest równa\[ \pi \](1 pkt.)
Promień stożka jest równy (1 pkt.)
Pole powierzchni całkowitej stożka jest równe\[ \pi \](1 pkt.)ZADANIE nr 34. (4 pkt.) Tomek i Kamil zbierali truskawki. Tomek pracując sam, zbiera\[1\]skrzynkę truskawek w\[3\]godziny. Gdyby chłopcy zbierali razem truskawki, to zajęłoby im to\[2\]godziny. Oblicz, w jakim czasie nazbierałby tę samą skrzynkę truskawek Kamil, gdyby pracował sam.Podaj odpowiedzi:
Kamil nazbierałby sam skrzynkę truskawek pracując godzin (4 pkt.)ZADANIE nr 35. (4 pkt.) Wyznacz współczynniki\[a,\;b, \;c\]funkcji kwadratowej o wzorze\[f(x) =ax^2 +bx+c \], wiedząc, że zbiorem wartości tej funkcji jest przedział\[(-\infty;\;2 \rangle \]oraz\[f(-1) = f(5) =- 7 \].Podaj odpowiedzi:
\[a=\](1 pkt.)
\[b=\](1 pkt.)
\[c=\](2 pkt.)
MATURA
2024
Z MATEMATYKI
