, 2014-02-28 
-
-
- INFORMATOR - ZAGADNIENIA
NIEOBOWIĄZUJĄCE NA MATURZE 2023 (liceum) - INFORMATOR - ZAGADNIENIA
NIEOBOWIĄZUJĄCE NA MATURZE 2023 (technikum) - DARMOWY PORADNIK O NAUCE
- PLANSZE I ZADANIA INTERAKTYWNE
- PEWNIAKI MATURALNE
- KSIĄŻKI ON-LINE
- TESTY ON-LINE
- MATURA Z MATEMATYKI 2024 ODPOWIEDZI
- ARKUSZE MATURALNE CKE
- TABLICE MATEMATYCZNE
- PODSTAWA PROGRAMOWA
- ZASADY MATURALNE - WAŻNE!
- KURS MATURALNY ON-LINE W FERIE
- WYPOŻYCZALNIA KSIĄŻEK ON-LINE
- ODBIERZ DARMOWĄ PŁYTĘ CD
- KURS EKSPRESOWY - INFORMACJE
- KURS EKSPRESOWY - ZAPISY
- WAŻNE INFORMACJE
- INFORMATOR - ZAGADNIENIA
-
SKLEPZAMÓWIENIA
GRUPOWE
Aby uzyskać przez szybką płatność DotPay dostęp do materiałów PREMIUM:
kliknij obok przycisk "dotpay" obok wybranej opcji i wykonaj szybką płatność.
kod dostępu zostanie wyświetlony po poprawnym zakończeniu transakcji i wysłany na podany adres e-mail.
Otrzymany kod wpisz w pole pod tabelką.
Aby uzyskać SMSem dostęp do materiałów PREMIUM:
wyślij krótki SMS na numer podany w tabeli obok wybranej opcji.
w zwrotnej widaomości sms otrzymasz kod dostępu do testów. Otrzymany kod wpisz w pole pod tabelką.
Usługa SMS dostępna w sieciach T-mobile, Plus, Play, Orange.Kod na 3 miesiące
koszt: 37,97 zł
(rabat 20%)47,46 złKod na pół roku
koszt: 49,97 zł
(rabat 20%)62,46 złPodane ceny usług są cenami brutto.
Właściciel serwisu:
Firma Edukacyjno-Wydawnicza ELITMAT Dariusz Kulma
ul. Okrzei 7
05-300 Mińsk Mazowiecki
elitmat@elitmat.pl
Usługi płatności internetowych obsługuje Eurokoncept, grupa Dotpay.
Regulamin Usług.
Reklamacja usługi Premium.
To jest tylko podgląd zadań. Aby rozwiązać maturę wybierz opcję:
MATURA PRÓBNA
MINI-MATURA POZIOM ROZSZERZONY.
Czas pracy: 45 minut .
Zadania rozwiązuj na kartce, następnie zaznaczaj odpowiedzi aby sprawdzić swój wynik.
TWÓJ CZAS:45:00 ZADANIE nr 1. (1 pkt.) Jeśli\[x,\;y,\;z \in R_{+}\]i\[k=\frac{xy+yz+xz}{xyz}\]i\[l=x+y+z\], to:Wybierz odpowiedź:
ZADANIE nr 2. (1 pkt.) Korzystając z danych na rysunku, można stwierdzić, że wartość wyrażenia\[ \sin \left( \frac{6 \alpha + 7 \beta - 20^{\circ}}{2} \right) \]jest równa: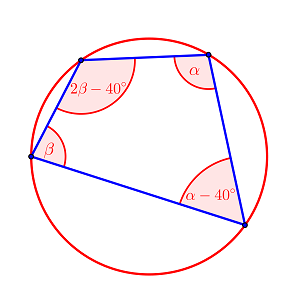
Wybierz odpowiedź:
ZADANIE nr 3. (2 pkt.) Liczba\[{2}\]jest trzykrotnym pierwiastkiem wielomianu\[W(x)=x^3+ax^2+bx+c\]. Zakoduj kolejno liczbę setek, dziesiątek i jedności sumy\[a^2+b^2+c^2\].Zakoduj odpowiedź w kratkach kolejno od lewej:ZADANIE nr 4. (3 pkt.) Punkt\[C (6;\;1) \]jest wierzchołkiem trójkąta\[ABC\]. Bok\[AB\]trójkąta zawiera się w prostej o równaniu\[y=2x+4 \], a wysokość poprowadzona z wierzchołka\[B\]zawiera się w prostej\[{-7x+y+1 =0}\]. Oblicz współrzędne wierzchołków\[A\]i\[B\]oraz pole trójkąta\[ABC\].Podaj odpowiedzi:Wpisz pierwszą współrzędną punktu \[A\](0.50 pkt.)Wpisz drugą współrzędną punktu \[A\](0.50 pkt.)Wpisz pierwszą współrzędną punktu \[B\](0.50 pkt.)Wpisz drugą współrzędną punktu \[B\](0.50 pkt.)Wpisz wartość pole \[\Delta ABC\;P=\]\[j^2 \](1.00 pkt.)ZADANIE nr 5. (5 pkt.) Naszkicuj wykres funkcji\[f(x)=|||x|-2|-1| \]. Określ liczbę rozwiązań równania\[f(x)=m \]względem parametru\[m\].Podaj odpowiedzi:Dla \[ m \in ( - \infty,\;0) \]liczba rozwiązań wynosi (1.00 pkt.)Dla \[ m =0 \]liczba rozwiązań wynosi (1.00 pkt.)Dla \[ m \in ( 0,\;1) \]liczba rozwiązań wynosi (1.00 pkt.)Dla \[ m =1 \]liczba rozwiązań wynosi (1.00 pkt.)Dla \[ m \in (1,\; \infty) \]liczba rozwiązań wynosi (1.00 pkt.)
MATURA
2024
Z MATEMATYKI
